모델-프리(Model-Free)
동적 프로그래밍(Dynamic Programming, DP)은 MDP 모델을 아는 상황에서의 계획입니다. 이와 반대로 보상 함수와 전이 확률과 같은 정보를 모르는 상황을 model-free 라고 하며 이는 경험(experience)을 통해야하며 에이전트와 환경의 상호작용을 통해 학습해야 하는 것입니다.
이러한 model-free 에서 정책 평가(policy evaluation) 혹은 예측(prediction) 방법으로는 몬테카를로 예측(MC prediction)과 시간차 예측(TD prediction)이 있습니다. 또한 여기서는 다루는 정책은 고정된 임의의 정책 $\pi$ 이라고 가정합니다.
몬테카를로 방법(Monte Carlo Method)
무작위로 샘플링을 반복하면 실제값에 근사한다는 방법론으로 계산하려는 값이 닫힌 형식으로 표현되지 않거나 복잡한 경우에 근사적으로 계산할 때 사용합니다. 몬테카를로 방법은 샘플이 많을 수록 대수의 법칙(law of large numbers)에 의해 실제 가치에 더 가까워진다는 것입니다.
아래 예제는 100번 던진 주사위와 1000번 던진 주사위의 차이를 보여줍니다.
import matplotlib.pyplot as plt
import numpy as np
dice = [1,2,3,4,5,6]
def roll_dice():
return np.random.choice(dice)
num_episode = 100
r = [roll_dice() for _ in range(num_episode)]
r = np.unique(r, return_counts=True)[1]
plt.bar(dice, r)
plt.title(str(num_episode) + ' episode')
plt.show()
num_episode = 1000
r = [roll_dice() for _ in range(num_episode)]
r = np.unique(r, return_counts=True)[1]
plt.bar(dice, r, color='red')
plt.title(str(num_episode) + ' episode')
plt.show()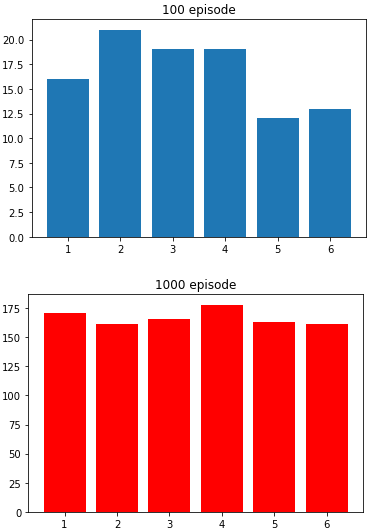
MC 예측(Monte Carlo Prediction)
MC 예측은 샘플 리턴의 평균값을 기반으로 가치 함수를 추정하는 것을 말합니다.
상태 가치 함수의 정의는 다음과 같습니다.
$v_\pi(s) \doteq \mathbb{E}_\pi[G_t|S_t=s]$
상태 $s$ 의 가치는 리턴의 기대값입니다. 따라서 $G_t$ 를 계속 샘플링하면 그 평균은 $v_\pi(s)$ 의 기댓값인 실제 가치(true value)에 수렴하게 된다는 것을 의미합니다. 이를 $G_t$ 는 $v_\pi(s)$ 의 불평 추정량(unbiased estimate)이라고 합니다.
각 상태에 대한 리턴을 구하면 다음과 같습니다.

각 상태마다 이러한 리턴 샘플을 모아서 평균을 구하면 각 상태의 가치는 실제 가치에 근사한다는 것입니다.
이를 식으로 나타내면 다음과 같습니다.
$v_\pi(s)={1 \over N} \displaystyle \sum_{i=1}^{N} G_i(s)$
여기서 문제는 1000번의 에피소드를 진행한다면 에피소드가 1000번 진행 후에 계산될 것이며 이는 매우 비효율적일 것입니다.
위의 식과 본질적으로 같으며 한 에피소드가 끝날 때마다 업데이트할 수 있는 식은 다음과 같습니다.
$V(S_t) \leftarrow (1-\alpha) * V(S_t) + \alpha * G_t$
$\alpha$ 의 값을 기준으로 기존의 값과 새로운 값을 섞어주는 것입니다. $\alpha$ 값을 작게 한다면 기존의 값을 크게 새로운 값을 작게하여 변화에 천천히 적용하는 것이라고 할 수 있습니다.
위 식을 정리하면 다음과 같습니다.
$V(S_t) \leftarrow V(S_t) + \alpha(G_t - V(S_t))$

또한 이러한 업데이트 방식을 샘플 업데이트(sample update)라고 합니다. 이는 샘플을 기반으로 한 것으로 DP 의 기댓값 업데이트(expected update)와는 다른 것입니다
구현
MC prediction 을 구현합니다.
# mc prediction(policy evaluation)
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import gym
env = gym.make('FrozenLake-v0', is_slippery=False)
gamma = 0.99
alpha = 0.1
v_table = np.zeros(env.observation_space.n)
num_episode = 10000
for i in range(num_episode):
memory = []
state = env.reset()
done = False
while not done:
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
memory.append((state, reward))
state = next_state
g = 0
for s, r in reversed(memory):
g = r + gamma*g
v_table[s] = v_table[s] + alpha*(g-v_table[s])
# print(v_table.reshape(4,4))
sns.heatmap(np.around(v_table.reshape(4, 4), 3), annot=True)
plt.title('MC Prediction', fontsize=18)
plt.show()
시간차 방법(Temporal Difference Method)
MC 는 단점이 있는데 에피소드가 끝날 때까지 기다려야 한다는 점입니다. 업데이트하기 위해서는 리턴이 필요한데 리턴은 에피소드가 끝나기 전까지는 알 수 없습니다. 즉 MC 는 종료되는 환경에서만 사용할 수 있는 것입니다. 이번에는 종료되지 않는 환경에도 온라인 학습이 가능한 TD 방법을 알아보겠습니다.
TD 예측(Temporal Difference Prediction)
TD 도 model-free 환경에서 경험을 통해 학습하는 방법이며 MC 와 DP 방법을 결합한 것입니다.
상태 가치 함수의 정의로부터 각 유도된 식은 다음과 같습니다.
$\begin{aligned}
v_{\pi}(s) & \doteq \mathbb{E}_{\pi}[G_t|S_t=s] & \scriptstyle{\text{MC}} \\
&=\mathbb{E}_{\pi}[R_{t+1} + \gamma v_{\pi}(S_{t+1})|S_t = s] & \scriptstyle{\text{TD}} \\
&=\displaystyle \sum_{a \in A} \pi(a|s) \displaystyle \sum_{s' \in S} P_{ss'}^a \left[ r + \gamma v_{\pi}(s') \right] & \scriptstyle{\text{DP}}
\end{aligned}$
MC 방법은 실제 리턴의 기댓값 대신에 샘플 리턴의 평균으로 기댓값에 근사하는 것입니다. DP 는 기댓값이 MDP 모델로부터 완전히 제공받는다고 볼 수 있으며 $v_{\pi}(S_{t+1})$ 대신 현재 추정된 가치 함수 $V(S_{t+1})$ 로부터 계산합니다. TD 는 두 방법을 모두 포함하는 것으로 샘플을 이용하며 실제 $v_{\pi}$ 대신 추정 $V$ 로 계산하는 것이라고 할 수 있으며 이를 부트스트랩(bootstrap)이라고 합니다.
업데이트 식은 다음과 같습니다.
$V(S_t) \leftarrow V(S_t) + \alpha(r_{t+1}+\gamma V(S_{t+1}) - V(S_t))$

구현
TD prediction 을 구현합니다.
# td prediction(policy evaluation)
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import gym
env = gym.make('FrozenLake-v0', is_slippery=False)
gamma = 0.99
alpha = 0.1
v_table = np.zeros(env.observation_space.n)
num_episode = 10000
for i in range(num_episode):
state = env.reset()
done = False
while not done:
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
td_target = reward + gamma * v_table[next_state]
v_table[state] = v_table[state] + alpha * (td_target - v_table[state])
state = next_state
# print(v_table.reshape(4,4))
sns.heatmap(np.around(v_table.reshape(4, 4), 3), annot=True)
plt.title('TD Prediction', fontsize=18)
plt.show()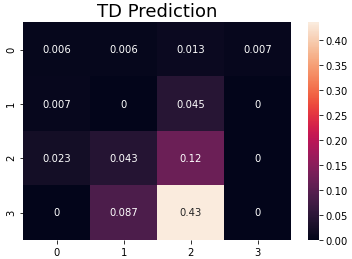
편향(Bias)
MC 와 TD 에서 사용하는 식을 비교합니다.
$\begin{aligned}
v_{\pi}(s) & \doteq \mathbb{E}_{\pi}[G_t|S_t=s] & \scriptstyle{\text{MC}} \\
&=\mathbb{E}_{\pi}[R_{t+1} + \gamma v_{\pi}(S_{t+1})|S_t = s] & \scriptstyle{\text{TD}} \\
\end{aligned}$
MC 방법은 리턴의 평균을 기반으로 리턴의 기댓값에 근사하고자하는 방법론으로 모든 상태를 방문하고 충분히 반복한다면 실제 가치에 수렴하게 될 것입니다. 즉 $G_t$ 는 $v_{\pi}(s)$ 의 불평 추정량으로 편향되지 않는 것입니다.
TD 방법의 경우에는 추정을 추정으로 계산하여 식 $r_{t+1} + \gamma v(S_{t+1})$ 에서 $v(S_{t+1})$ 에 대한 계산은 추정된 $V$ 를 이용합니다. $r_{t+1} + \gamma v_\pi(s_{t+1})$ 는 $v_{\pi}(s)$ 의 불편 추정량이지만 $r_{t+1} + \gamma V(S_{t+1})$ 은 편향되었다는 것입니다.
분산(Variance)
MC 방법은 한 에피소드동안 발생된 샘플의 리턴을 이용해 업데이트가 이루어집니다.

방문한 상태의 많은 샘플에 대해 계산하기 때문에 분산 혹은 변동성이 크다는 것입니다. 즉 현재 상태에서 다음 상태로 가는데 한 번에 갈 수도 있지만 다른 상태를 거쳐서 갈 수도 있기 때문입니다.
반면 TD 방법은 현재 상태 $S_t$ 는 단일 샘플 $r_{t+1}$ 과 $V(S_{t+1})$ 로 업데이트가 가능하기 때문에 분산이 적다고 할 수 있습니다. 또한 단일 샘플을 이용하는 계산을 TD(0) 혹은 1-스텝 TD 라고합니다.

n-스텝 예측(n-Step Prediction)
n-스텝 TD 는 1-스텝 TD 와 MC 양극단의 중간쯤 되는 방법으로 n-스텝 리턴을 통해 업데이트합니다.

상태 $S_t$ 의 가치 추정값 $V(S_t)$ 에 대해 한 에피소드의 궤적 $S_t, R_{t+1}, S_{t+1}, R_{t+2}, \dots, R_T, S_T$ 을 이용해서 업데이트한다고 가정합니다.
이에 대한 리턴은 다음과 같습니다.
$G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma ^{T-t-1} R_T$
n-스텝 리턴을 나타내면 다음과 같습니다.
$G_{t:t+1} \doteq R_{t+1} + \gamma V_t(S_{t+1})$
$G_{t:t+2} \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 V_{t+1}(S_{t+2})$
$\dots$
$G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n V_{t+n-1}(S_{t+n})$
스텝 n 값을 1로하면 1-스텝 TD이며 무한히 크게하면 그냥 리턴이 됩니다. 즉 n 값에 따라 미래가 과거에 영향을 주는 정도를 조절할 수 있으며 n 값을 크게하면 MC 방법의 성질과 가까워지므로 분산이 커지게 됩니다. 적당한 n 값을 사용하면 MC 와 TD 의 장점을 모두 살려 편향과 분산을 조절할 수 있습니다.
다음은 어떤 환경의 10번의 에피소드에 대하며 100번 반복한 실험의 결과로 실제값과 예측값의 평균제곱오차를 나타냅니다.

n 의 중간 값을 사용한 방법이 좋은 결과를 나타내고 있습니다.
n-스텝 리턴을 이용한 업데이트식은 다음과 같습니다.
$V(S_t) \leftarrow V(S_t) + \alpha(G_{t:t+n} - V(S_t))$
참고로 A3C 알고리즘에서 사용된 n-스텝 TD 입니다.

에피소드 종료 혹은 n 값에 해당하는 $t_{max}$ 에 도달하면 그 이전까지 모았던 샘플 궤적 $s_t$, $a_t$, $r_t$, ..., $s_n$, $a_n$, $r_n$ 을 역방향으로 계산하여 각 상태의 리턴과 상태의 추정 가치의 오차를 줄여나가는 과정입니다.
구현
n-스텝 TD prediction 을 구현합니다.
# n-step td prediction(policy evaluation)
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import gym
env = gym.make('FrozenLake-v0', is_slippery=False)
n = 8
gamma = 0.99
alpha = 0.1
v_table = np.zeros(env.observation_space.n)
num_episode = 10000
for i in range(num_episode):
memory = []
state = env.reset()
done = False
while not done:
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
memory.append((state, reward))
if done or len(memory) == n:
if done:
g = 0
else:
next_action = get_action(e, next_state)
g = v_table[next_state]
for s, r in reversed(memory):
g = r + gamma * g
v_table[s] += alpha * (g - v_table[s])
memory.clear()
state = next_state
# print(v_table.reshape(4,4))
sns.heatmap(np.around(v_table.reshape(4, 4), 3), annot=True)
plt.title('n-Step TD Prediction', fontsize=18)
plt.show()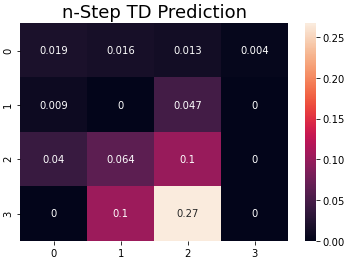
'머신러닝 > 강화학습' 카테고리의 다른 글
| Model-Free Control (0) | 2020.11.13 |
|---|---|
| 소프트맥스 회귀(Softmax Regression) (2) (0) | 2020.11.12 |
| OpenAI Gym (0) | 2020.11.09 |
| 동적 프로그래밍(Dynamic Programming) (0) | 2020.11.06 |
| 벨만 방정식(Bellman Equation) (0) | 2020.11.04 |