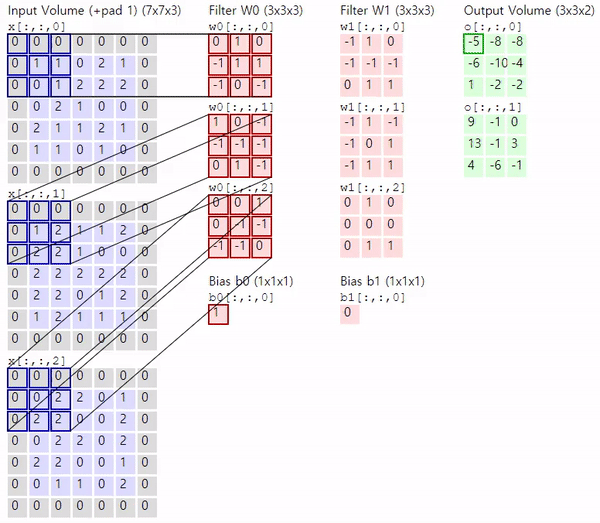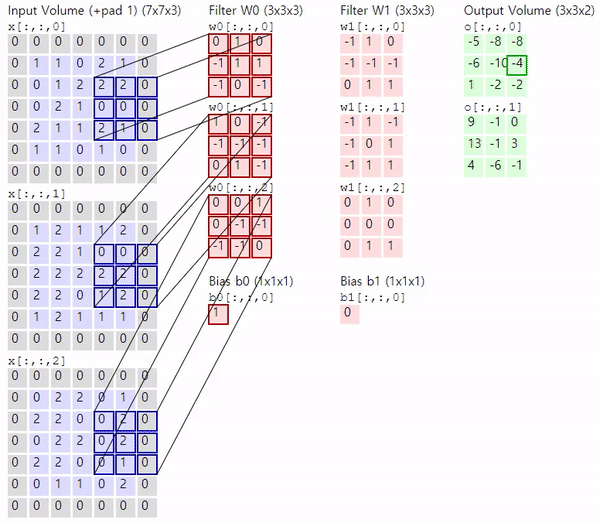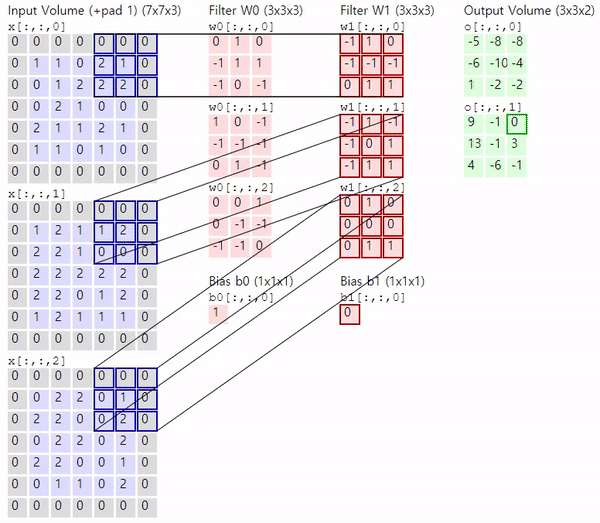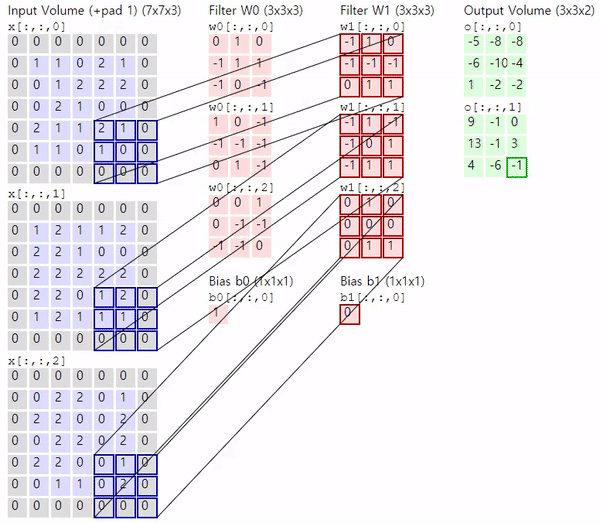
오토인코더(AutoEncoder, AE)
오토인코더는 인코더(encoder)와 디코더(decoder)로 이루어진 신경망입니다. 인코더는 고차원의 입력 데이터를 저차원의 표현 벡터(representation vector)로 압축하며, 디코더는 압축을 해제하여 복원합니다. 즉 신경망의 출력은 입력 데이터에 대해 재구성된 것입니다. 이러한 입력과 출력 간의 손실을 최소화하는 방향으로 학습하며 레이블없는 데이터를 사용하는 비지도학습(unsupervised learning)입니다.

군집화(Clustering)
인코더의 출력은 고차원의 입력 데이터에 대한 압축되어진 특징이라고 할 수 있습니다. 이를 2차원 벡터로 하여 산점도로 표현하면 다음과 같습니다.

이는 비슷한 특징을 가진 데이터 간에 군집을 이루며 분류되는 것입니다.
이러한 특징을 이용하여 입력 데이터에 대해 재구성하는 것이 디코더의 역할입니다.
구현
오토인코더 모델을 구현합니다,
MNIST 데이터셋을 불러옵니다.
import numpy as np
from tensorflow.keras import datasets
(x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()
x_train = x_train.reshape(-1, 28, 28, 1)
x_test = x_test.reshape(-1, 28, 28, 1)
print(x_train.shape)
print(x_test.shape)
신경망을 정의합니다.
import numpy as np
import tensorflow as tf
class Encoder:
def __init__(self, input, training):
with tf.name_scope('layer'):
conv1 = tf.layers.conv2d(input, 32, 3, 1, padding='same')
conv1 = tf.layers.batch_normalization(conv1, training=training)
conv1 = tf.nn.leaky_relu(conv1)
conv2 = tf.layers.conv2d(conv1, 64, 3, 2, padding='same')
conv2 = tf.layers.batch_normalization(conv2, training=training)
conv2 = tf.nn.leaky_relu(conv2)
conv3 = tf.layers.conv2d(conv2, 64, 3, 2, padding='same')
conv3 = tf.layers.batch_normalization(conv3, training=training)
conv3 = tf.nn.leaky_relu(conv3)
conv4 = tf.layers.conv2d(conv3, 64, 3, 1, padding='same')
conv4 = tf.layers.batch_normalization(conv4, training=training)
conv4 = tf.nn.leaky_relu(conv4)
flat = tf.layers.flatten(conv4)
with tf.name_scope('output'):
self.output = tf.layers.dense(flat, 2)
class Decoder:
def __init__(self, input, training):
with tf.name_scope('layer'):
fc = tf.layers.dense(input, 3136)
reshape = tf.reshape(fc, [-1, 7, 7, 64])
conv_tran1 = tf.layers.conv2d_transpose(reshape, 64, 3, 1, padding='same')
conv_tran1 = tf.layers.batch_normalization(conv_tran1, training=training)
conv_tran1 = tf.nn.leaky_relu(conv_tran1)
conv_tran2 = tf.layers.conv2d_transpose(conv_tran1, 64, 3, 2, padding='same')
conv_tran2 = tf.layers.batch_normalization(conv_tran2, training=training)
conv_tran2 = tf.nn.leaky_relu(conv_tran2)
conv_tran3 = tf.layers.conv2d_transpose(conv_tran2, 64, 3, 2, padding='same')
conv_tran3 = tf.layers.batch_normalization(conv_tran3, training=training)
conv_tran3 = tf.nn.leaky_relu(conv_tran3)
conv_tran4 = tf.layers.conv2d_transpose(conv_tran3, 32, 3, 1, padding='same')
conv_tran4 = tf.layers.batch_normalization(conv_tran4, training=training)
conv_tran4 = tf.nn.leaky_relu(conv_tran4)
with tf.name_scope('output'):
self.output = tf.layers.conv2d_transpose(conv_tran4, 1, 3, 1, padding='same', activation=tf.nn.sigmoid)
class Model:
def __init__(self, lr=1e-3):
tf.reset_default_graph()
with tf.name_scope('input'):
self.input = tf.placeholder(tf.float32, [None, 28, 28, 1])
self.training = tf.placeholder(tf.bool)
with tf.name_scope('preprocessing'):
input_norm = self.input / 255.0
self.encoder = Encoder(input_norm, self.training)
self.decoder = Decoder(self.encoder.output, self.training)
with tf.name_scope('loss'):
self.loss = tf.losses.mean_squared_error(input_norm, self.decoder.output)
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.name_scope('optimizer'):
train_op = tf.train.AdamOptimizer(lr).minimize(self.loss)
self.train_op = tf.group([train_op, update_ops])
self.sess = tf.Session()
self.sess.run(tf.global_variables_initializer())
def encode(self, x):
return self.sess.run(self.encoder.output, {self.input: x, self.training: False})
def decode(self, x):
return self.sess.run(self.decoder.output, {self.input: x, self.training: False})
def train(self, x_train, epochs, batch_size=32):
data_size = len(x_train)
for e in range(epochs):
t_l = []
idx = np.random.permutation(np.arange(data_size))
_x_train = x_train[idx]
for i in range(0, data_size, batch_size):
si, ei = i, i + batch_size
if ei > data_size:
ei = data_size
x_batch = _x_train[si:ei, :, :]
_, loss = self.sess.run([self.train_op, self.loss], {self.input: x_batch, self.training: True})
t_l.append(loss)
print('epoch:', e + 1, '/ loss:', np.mean(t_l))
모델을 학습합니다.
model = Model(lr=5e-4)
model.train(x_train, epochs=10)epoch: 1 / loss: 0.050720453
epoch: 2 / loss: 0.044929303
epoch: 3 / loss: 0.043423332
epoch: 4 / loss: 0.042490218
epoch: 5 / loss: 0.04188228
epoch: 6 / loss: 0.041391663
epoch: 7 / loss: 0.041031186
epoch: 8 / loss: 0.040655673
epoch: 9 / loss: 0.04040248
epoch: 10 / loss: 0.040120468
테스트 데이터로 2차원 표현 벡터를 산점도로 나타내고 무작위 데이터의 포인트를 확인합니다.
import matplotlib.pyplot as plt
encoder_output = model.encode(x_test)
plt.figure(figsize=(16, 8))
plt.scatter(encoder_output[:, 0], encoder_output[:, 1], c=y_test, cmap=plt.get_cmap('Paired'), s=10)
plt.colorbar()
plt.title('Encoder output')
n = 4
idx = np.random.choice(range(len(x_test)), n)
encoder_output = model.encode(x_test[idx])
decoder_output = model.decode(x_test[idx])
plt.scatter(encoder_output[:, 0], encoder_output[:, 1], c='black', s=100)
plt.show()
fig, axs = plt.subplots(n, 2, constrained_layout=True, sharey=True, figsize=(5, 5))
for i in range(n):
axs[i][0].imshow(x_test[idx][i], aspect='auto', cmap='gray')
axs[i][0].axis('off')
axs[i][1].imshow(decoder_output[i], aspect='auto', cmap='gray')
axs[i][1].axis('off')
if i == 0:
axs[i][0].set_title('True')
axs[i][1].set_title('Prediction')
plt.show()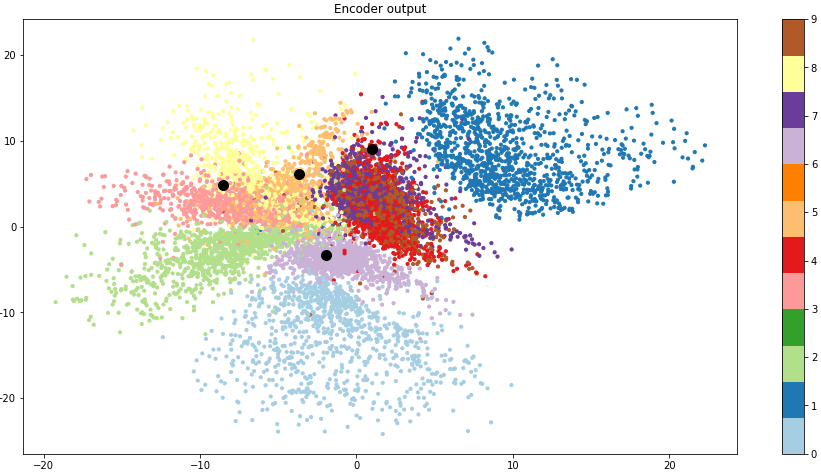
군집화가 명확하지 않은 영역에 대한 복원은 잘 이루어지지 않는 것을 볼 수 있습니다.

'머신러닝 > 딥러닝' 카테고리의 다른 글
| 드롭아웃(Dropout) (0) | 2021.02.09 |
|---|---|
| 가중치 규제(Weight Regularization) (0) | 2021.02.09 |
| 배치 정규화(Batch Normalization) (0) | 2021.02.09 |
| 가중치 초기화(Weight Initialization) (0) | 2021.02.08 |
| LSTM(Long Short-Term Memory) (0) | 2021.02.03 |