동적 프로그래밍(Dynamic Programming, DP)
동적 프로그래밍은 MDP 와 같은 환경의 모델이 완벽히 주어졌을 때 푸는 방법론입니다. 즉 보상 함수와 전이 확률과 같은 정보를 알 때 시뮬레이션을 통해 계획(planning) 을 세우는 것이라고 할 수 있습니다.
MDP 를 푼다는 것은 크게 예측(prediction)과 제어(control) 문제로 나누어집니다.
prediction 은 주어진 정책 $\pi$ 에 대해 가치 함수를 계산하여 정책을 평가하는 것이라고 할 수 있으며 control 은 정책 평가를 통해 얻은 가치 함수를 이용해 정책을 개선하는 것이라고 할 수 있습니다.
정책 평가(Policy Evaluation)
정책이 좋은 정책인지 나쁜 정책인지 평가하는 것은 정책 $\pi$ 에 대한 가치 함수 $v_{\pi}$ 를 구하는 것과 같습니다. (아래에서 다루는 policy iteration 을 통해 직관적으로 이해할 수 있습니다.)
정책 $\pi$ 에 대한 $v_{\pi}$ 계산은 벨만 기대 방정식을 이용합니다.
$v_{\pi}(s) = \displaystyle \sum_{a \in A} \pi(a|s) \displaystyle \sum_{s' \in S} P_{ss'}^a \left[ r + \gamma v_{\pi}(s') \right]$
다음과 같은 episodic MDP 로 정의된 4x4 그리드월드 환경이 있습니다.

양쪽 끝의 종료 상태가 두 개있고 이를 제외한 나머지 상태는 4개의 행동을 취할 수 있습니다. 4개의 행동에 대해 동일한 확률을 가지는 정책이며 행동에 대한 보상은 모두 -1입니다. 가장자리 상태에서 주어진 환경을 벗어나는 행동을 하면 제자리로 돌아오며 상태 전이는 확정적으로 100% 확률로 전이됩니다. 또한 에피소딕 문제이므로 $\gamma=1$ 로 합니다.
초기에는 종료 상태 포함 모든 상태의 가치는 0으로 초기화했다고 가정합니다.

첫 번째 스텝에서 1번 상태의 가치를 계산하면 다음과 같습니다.
$4 * 0.25(-1 + 1 * 0) = -1$
2번에서 14번 또한 동일하게 계산되며 업데이트된 모든 상태는 다음과 같습니다.

이처럼 새로운 가치는 이전 가치와 즉각적인 보상의 기댓값을 이용하여 구하는데 이것을 기댓값 업데이트(expected update)라고 합니다. 이 업데이트는 샘플이 아닌 가능한 전체 상태에 대한 기댓값에 기반하여 이루어 지는 것입니다.
두 번째 스텝에서는 1번 상태의 가치를 계산하면 다음과 같습니다.
$0.25(-1 + 1 * 0) + 3 * 0.25(-1 + 1 * -1) = -1.75$
왼쪽으로 가는 행동에 대한 계산은 종료 상태의 가치는 0이므로 $0.25(-1 + 1 * 0)$ 으로 계산한 것이고 위로 가는 행동은 제자리로 돌아오기 때문에 자기 상태의 가치를 이용합니다. 따라서 위, 아래, 오른쪽 모두 동일하게 $0.25(-1 + 1 * -1)$ 으로 계산한 것입니다.
2번 상태의 가치의 계산은 다음과 같습니다.
$4 * 0.25(-1 + 1 * -1) = -2$
계산된 전체 가치는 다음과 같습니다.

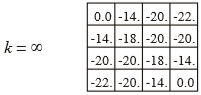
이 과정을 반복하다 보면 각 상태의 값은 수렴하게 되는데 이를 실제 가치(true value) 라고 합니다.
정책 개선(Policy Improvement)
정책 개선 단계는 정책 평가에서 구한 가치 함수를 이용해 그리디 정책(greedy policy)을 생성합니다. 이는 각 상태에서 다음 상태가 최대 가치를 가지는 행동을 선택하게 정책을 수정하는 과정인 것입니다.
$\pi'=\text{greedy}(v_\pi)$
정책 평가의 첫 번째 스텝의 가치 함수를 이용해서 그리디 정책을 생성하면 다음과 같습니다.

모든 상태가 동일한 가치이기 때문에 여전히 랜덤한 정책을 갖게 됩니다.
두 번째 스텝의 가치 함수를 이용해보면 다음과 같습니다.

종료 상태와 근접한 상태의 행동 선택이 수정되었습니다.
실제 가치 함수에 수렴하면 최종적으로 다음과 같은 정책으로 수정됩니다.
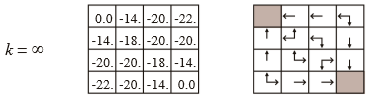
정책 반복(Policy Iteration)
정책 평가와 정책 개선을 번갈아 수행하여 최적 정책 $\pi_*$ 및 최적 가치 함수 $v_*$ 로 수렴할 때까지 반복하는 것을 말합니다.

policy iteration 의 사이클은 다음과 같이 나타낼 수 있습니다.
$\pi_0 \overset {E} \longrightarrow v_{\pi_0} \overset {I} \longrightarrow \pi_1 \overset {E} \longrightarrow v_{\pi_1} \overset {I} \longrightarrow \pi_2 \overset {E} \longrightarrow \cdots \overset {I} \longrightarrow \pi_* \overset {E} \longrightarrow v_*$
정책 $\pi_0$ 으로 시작해서 정책 평가를 통해 $v_{\pi_0}$ 를 계산하고 이를 이용해서 정책 개선을 하면 $\pi_0$ 보다 향상된 $\pi_1$ 가 될 것입니다. 이 과정을 반복하면 최적 정책 $\pi_*$ 에 수렴할 것이고 이를 통해 계산된 가치 함수는 최적 가치 함수 $v_*$ 가 될 것입니다.
policy iteration 알고리즘은 다음과 같습니다.

구현
policy iteration 을 구현합니다.
import numpy as np
SIZE = 4
# SIZE = 3
T = [(0, 0), (3, 3)]
# T = [(3, 2), (1, 1)]
K = 3
R = -1
P = 0.25
GAMMA = 1
ACTION = ['left', 'up', 'down', 'right']
def get_value(table, row, col, action):
if action == 'up':
if row != 0:
row -= 1
elif action == 'down':
if row != SIZE-1:
row += 1
if action == 'left':
if col != 0:
col -= 1
elif action == 'right':
if col != SIZE-1:
col += 1
return table[row][col]
def view_policy(policy):
for row in range(SIZE):
line = []
for col in range(SIZE):
if (row, col) in T:
line.append('T')
else:
idx = policy[row][col]
line.append(ACTION[idx])
print(' | '.join(line))
def policy_evaluation(policy):
table = np.zeros((SIZE, SIZE))
for _ in range(100):
pre_table = table.copy()
for row in range(SIZE):
for col in range(SIZE):
if (row, col) in T:
continue
update_value = 0
for idx, prob in enumerate(policy[row][col]):
update_value += prob * (R + GAMMA*get_value(pre_table, row, col, ACTION[idx]))
table[row][col] = update_value
return table
def policy_improvement(table):
policy = np.zeros((SIZE, SIZE, len(ACTION)))
for row in range(SIZE):
for col in range(SIZE):
q = []
for action in ACTION:
q.append(R + GAMMA*get_value(table, row, col, action))
idx = np.argmax(q)
policy[row, col, idx] = 1.
return policy
def policy_iteration():
policy = np.ones((SIZE, SIZE, len(ACTION))) * P
for k in range(K):
print('\n\nk=',k)
print('-'*50)
table = policy_evaluation(policy)
print(table)
print('-'*50)
policy = policy_improvement(table)
view_policy(np.argmax(policy, axis=2))
print('Gridworld size : {} x {}'.format(SIZE, SIZE))
print('Terminate state:', *T)
policy_iteration()Gridworld size : 4 x 4
Terminate state: (0, 0) (3, 3)
k= 0
--------------------------------------------------
[[ 0. -13.94260509 -19.91495107 -21.90482522]
[-13.94260509 -17.92507693 -19.91551999 -19.91495107]
[-19.91495107 -19.91551999 -17.92507693 -13.94260509]
[-21.90482522 -19.91495107 -13.94260509 0. ]]
--------------------------------------------------
T | left | left | left
up | left | left | down
up | up | right | down
up | right | right | T
k= 1
--------------------------------------------------
[[ 0. -1. -2. -3.]
[-1. -2. -3. -2.]
[-2. -3. -2. -1.]
[-3. -2. -1. 0.]]
--------------------------------------------------
T | left | left | left
up | left | left | down
up | left | down | down
up | right | right | T
k= 2
--------------------------------------------------
[[ 0. -1. -2. -3.]
[-1. -2. -3. -2.]
[-2. -3. -2. -1.]
[-3. -2. -1. 0.]]
--------------------------------------------------
T | left | left | left
up | left | left | down
up | left | down | down
up | right | right | T
가치 반복(Value Iteration)
policy iteration 은 최적 정책을 찾기 위해 정책 평가와 개선의 과정을 반복하는 것이었습니다. 하지만 정책 평가는 많은 비용이 발생하는 계산으로 $v_{\pi}$ 가 수렴하기 위해서는 많은 반복을 통해야만 하며 정책 이터레이션의 각 단계마다 계산해야하는 과정입니다. 이와 같은 정책 평가의 반복되는 과정은 중간에 중단된다 하더라도 정책 이터레이션의 수렴성이 보장되는데 이 같은 성질을 이용하여 적은 수의 반복으로 최적의 정책을 찾고자하는 것이 value iteration 입니다.
value iteration 은 벨만 최적 방정식을 이용합니다.
$\begin{aligned}
v_{k+1}(s) & \doteq {\underset {a} {\text{max}} } \, \mathbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) \, | \, S_t=s, A_t=a] \\
& = {\underset {a} {\text{max}} } \displaystyle \sum_{s',r} p(s',r \, | \, s,a)\Big[ r + \gamma v_k(s') \Big]
\end{aligned}$
모든 상태 $s \in \mathcal{S}$ 에 대해 성립하며 임의의 $v_0$ 에 대해 $v_*$ 를 보장하는 조건하에 수열 ${v_k}$ 는 $v_*$ 로 수렴하는 것입니다.
벨만 최적 방정식은 $\underset {a} {\text{max}}$ 이 붙어 최적의 행동만을 고려한 계산입니다. 이것은 정책 개선과 유사하다고 할 수 있습니다. 따라서 value iteration 은 중단된 정책 평가와 정책 개선을 결합하는 것으로 적은 수의 반복으로도 policy iteration 과 같은 기능을 하게 되는 것입니다.
value iteration 알고리즘은 다음과 같습니다.

구현
value iteration 을 구현합니다.
# value iteration
import numpy as np
SIZE = 4
T = [(0, 0), (3, 3)]
K = 4
R = -1
GAMMA = 1
ACTION = ['left', 'up', 'down', 'right']
def get_value(table, row, col, action):
if action == 'up':
if row != 0:
row -= 1
elif action == 'down':
if row != SIZE-1:
row += 1
if action == 'left':
if col != 0:
col -= 1
elif action == 'right':
if col != SIZE-1:
col += 1
return table[row][col]
def get_policy(table):
policy = np.zeros((SIZE, SIZE, len(ACTION)))
for row in range(SIZE):
for col in range(SIZE):
q = []
for action in ACTION:
q.append(R + GAMMA*get_value(table, row, col, action))
idx = np.argmax(q)
policy[row, col, idx] = 1.
return policy
def view_policy(policy):
for row in range(SIZE):
line = []
for col in range(SIZE):
if (row, col) in T:
line.append('T')
else:
idx = policy[row][col]
line.append(ACTION[idx])
print(' | '.join(line))
def value_iteration():
table = np.zeros((SIZE, SIZE))
for k in range(K):
pre_table = table.copy()
for row in range(SIZE):
for col in range(SIZE):
if (row, col) in T:
continue
next_values = []
for action in ACTION:
value = R + GAMMA*get_value(pre_table, row, col, action)
next_values.append(value)
table[row][col] = np.max(next_values)
print('\n\nk=', k)
print('-'*20)
print(table)
print('\n\n')
policy = get_policy(table)
view_policy(np.argmax(policy, axis=2))
value_iteration()k= 0
--------------------
[[ 0. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. -1.]
[-1. -1. -1. 0.]]
k= 1
--------------------
[[ 0. -1. -2. -2.]
[-1. -2. -2. -2.]
[-2. -2. -2. -1.]
[-2. -2. -1. 0.]]
k= 2
--------------------
[[ 0. -1. -2. -3.]
[-1. -2. -3. -2.]
[-2. -3. -2. -1.]
[-3. -2. -1. 0.]]
k= 3
--------------------
[[ 0. -1. -2. -3.]
[-1. -2. -3. -2.]
[-2. -3. -2. -1.]
[-3. -2. -1. 0.]]
T | left | left | left
up | left | left | down
up | left | down | down
up | right | right | T
'머신러닝 > 강화학습' 카테고리의 다른 글
| Model-Free Prediction (0) | 2020.11.09 |
|---|---|
| OpenAI Gym (0) | 2020.11.09 |
| 벨만 방정식(Bellman Equation) (0) | 2020.11.04 |
| 마르코프 결정 프로세스(Markov Decision Process) (0) | 2020.11.04 |
| 강화 학습(Reinforcement Learning) (0) | 2020.11.04 |