행동 가치 함수(Action Value Function)
model-free 에서 가치 함수 $V(s)$ 를 추정하는 방법에는 MC 와 TD 가 있었습니다. 하지만 이것만으로는 각 상태에서 어떤 행동을 선택해야 하는지 알 수 없습니다. 따라서 정책 개선 또는 제어(control)하기 위해서는 상태 가치 함수 $V(s)$ 대신에 행동 가치 함수 $Q(s,a)$ 를 구해야 합니다. $Q(s,a)$ 를 이용하면 높은 가치를 가지는 행동을 선택할 수 있기 때문입니다. 또 이러한 행동 가치 함수를 이용한 제어를 행동 가치 기반 방법론이라고 합니다.
MC prediction 을 통해 $Q(s,a)$ 를 구하고 이를 이용하여 greedy 정책을 생성합니다.
import time
import numpy as np
import gym
env = gym.make('FrozenLake-v0', is_slippery=False)
q_table = np.zeros((env.observation_space.n, env.action_space.n))
gamma = 0.99
alpha = 0.1
num_episode = 10000
for i in range(num_episode):
memory = []
state = env.reset()
done = False
while not done:
action = env.action_space.sample()
next_state, reward, done, _ = env.step(action)
memory.append((state, action, reward))
state = next_state
g = 0
visted = []
for s, a, r in reversed(memory):
if s in visted: # 1-visited
continue
g = r + gamma*g
q_table[s, a] = q_table[s, a] + alpha*(g-q_table[s, a])
visted.append(s)
state = env.reset()
done = False
while not done:
env.render()
time.sleep(0.2)
action = np.argmax(q_table[state])
state, reward, done, _ = env.step(action)
if reward == 1:
print('success')
else:
print('failure')
# print(q_table)success
작은 환경의 경우에는 무작위 정책으로도 실제 가치(true value)에 근사할 만큼 충분한 탐색이 가능했습니다. 하지만 복잡한 환경에서는 무작위 정책으로는 모든 상태를 탐색하기 어려울 것입니다. 모든 상태를 탐색하지 않으면 실제 가치에 근사할 수 없게 됩니다.
입실론 그리디($\epsilon$-Greedy)
무작위 행동과 최선의 행동 사이에 확률적으로 선택함으로써 지속적이고 충분한 탐색(exploration)과 이용(exploitaion)을 가능하게 하여 정책을 개선하는 방법입니다.
$f(n)= \begin{cases} 1-\epsilon \text{ if } a^* = & \mbox{ $\underset{a} {argmax}$ q(s,a)} \\ \epsilon & \mbox{ otherwise} \end{cases}$
$\epsilon$-greedy 의 $\epsilon$ 는 무작위 행동을 선택할 확률을 나타내는 것이며 이를 점점 감소시키는 전략을 사용하는데 이를 decaying $\epsilon$-greedy 라고 합니다.
그 목적은 $Q$ 테이블이 학습되지 않은 초기에는 랜덤한 행동을 선택할 확률을 높게하여 탐색을 더 많이 하고 그 확률을 점점 감소시키고 최선의 행동을 선택할 확률을 증가시켜 탐색 반경을 넓히는 것입니다.
단순하게는 전체 에피소드에 대한 현재 에피소드 비율을 빼줌으로써 구현할 수 있습니다.
import numpy as np
import matplotlib.pyplot as plt
num_episode = 100
start_epsilon = 1
def decay_epsilon(episode):
e = start_epsilon - episode / num_episode
return e
episode = np.arange(num_episode)
epsilon = decay_epsilon(episode)
plt.plot(epsilon)
plt.title('e-greedy')
plt.xlabel('episode')
plt.ylabel('e')
plt.show()
일반적으로 다음과 같이 $\epsilon$ 에 최소값을 지정하는 방식을 많이 사용합니다.
import numpy as np
import matplotlib.pyplot as plt
num_episode = 100
start_epsilon = 1
end_epsilon = 0.1
def decay_epsilon(episode):
e = start_epsilon - episode / num_episode
return e if e > end_epsilon else end_epsilon
epsilon = []
for i in range(num_episode):
epsilon.append(decay_epsilon(i))
plt.plot(epsilon, 'red')
plt.title('e-greedy')
plt.xlabel('episode')
plt.ylabel('e')
plt.show()
MC Control
이러한 $\epsilon$-greedy 를 이용해서 정책을 개선해야 합니다.
그전에 DP 의 policy iteration 을 되새겨보면 어떤 정책 $\pi$ 이 주어지고 정책 평가 단계에서 반복을 통해 수렴된 $v_{\pi}(s)$ 를 구하고 정책 개선 단계에서 $v_{\pi}(s)$ 를 이용해서 최선의 행동을 선택하는 greedy 정책을 생성하고 이 과정을 반복하여 최적의 정책 $\pi_*$ 을 구하는 것이었습니다.
이것이 가능한 이유는 DP 는 MDP 모델이 완벽히 주어지며 가능한 모든 상태에 대하여 계산하기 때문입니다. 하지만 model-free 환경에서는 MDP 를 모르기 때문에 DP 의 방식과는 차이가 있습니다.
먼저 정책 평가 단계에서 $Q(s,a)$ 를 수렴할 때까지 반복하지 않으며 정책 개선 단계에서 바로 greedy 정책을 생성하지 않습니다. 이는 $\epsilon$-greedy 를 사용하는 것과 관계가 있는 것입니다.
$\epsilon$-greedy 를 포함하는 policy iteration 과정을 보면 $\epsilon$ 값이 1인 정책을 생성하고 이 정책은 랜덤한 행동만을 선택합니다. 또한 이 정책이 만들어내는 궤적을의 샘플을 이용하여 $Q(s,a)$ 를 계산합니다. $\epsilon$ 값이 0.9인 정책은 90% 확률로 무작위 행동과 10% 확률로 이전 정책($\epsilon=1$)을 통해 계산된 $Q(s,a)$ 의 최선의 행동을 선택합니다. 이를 반복하며 최종적으로 $\epsilon$ 값이 0이 되면 greedy 정책이며 지금까지 계산된 $Q(s,a)$ 를 이용하여 최선의 행동만을 선택만을 하게 됩니다.
구현
MC control 을 구현합니다.
import time
import matplotlib.pyplot as plt
import numpy as np
import gym
env = gym.make('FrozenLake-v0', is_slippery=False)
q_table = np.zeros((env.observation_space.n, env.action_space.n))
gamma = 0.99
alpha = 0.1
success = []
num_episode = 2000
for i in range(num_episode):
memory = []
e = 1 - i / num_episode
state = env.reset()
done = False
while not done:
if np.random.rand() < e:
action = env.action_space.sample()
else:
action = np.argmax(q_table[state])
next_state, reward, done, _ = env.step(action)
memory.append((state, action, reward))
state = next_state
success.append(reward)
g = 0
visted = []
for s, a, r in reversed(memory):
if s in visted: # 1-visited
continue
g = r + gamma*g
q_table[s, a] = q_table[s, a] + alpha*(g-q_table[s, a])
visted.append(s)
plt.plot(range(num_episode), success)
plt.show()
print('success rate:', np.mean(success))
성공률이 높은 수치는 아니지만 $\epsilon$ 값이 감소함에 따라 성공이 증가하는 것을 볼 수 있습니다.
TD Control
MC 대신 TD 를 이용할 수 있습니다. TD 는 종료되지 않는 환경에서도 온라인 학습이 가능하다는 장점을 가지고 있습니다.
TD 또한 $V(s)$ 대신 $Q(s,a)$ 를 구해야 하며 업데이트 방식에 따라 SARSA 와 Q-learning 으로 나누어집니다.
SARSA
SARSA 는 on-policy TD control 알고리즘으로 벨만 기대 방정식을 이용합니다.
$Q(s,a)$ 에 대한 벨만 기대 방정식과 업데이트 식은 다음과 같습니다.
$q_{\pi}(s,a) = \mathbb{E}_{\pi}[r_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1}) | S_t=s, A_t=a]$
$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R+\gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right]$
$Q(S_t,A_t)$ 를 업데이트하기 위해서는 다음 상태 $S_{t+1}$ 와 다음 행동 $A_{t+1}$ 에 대한 정보가 있어야 합니다. $A_{t+1}$ 은 현재의 정책이 다음 상태에 대해 선택한 행동입니다.
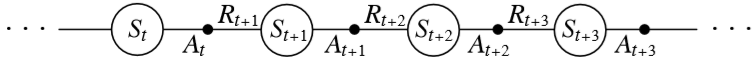
상태 $S$ 에서 행동 $A$ 를 취하면 보상 $R$ 과 다음 상태 $S$ 을 얻고 여기서 또 다음 상태에서 다음 행동 $A$ 을 선택해서 SARSA 라는 이름이 지어진 것입니다.
SARSA 알고리즘은 다음과 같습니다.

구현
SARSA 알고리즘을 구현합니다.
import matplotlib.pyplot as plt
import numpy as np
import gym
env = gym.make('FrozenLake-v0', is_slippery=False)
num_episode = 2000
gamma = 0.99
alpha = 0.01
q_table = np.zeros((env.observation_space.n, env.action_space.n))
success = []
def get_action(e, state):
if np.random.rand() < e:
return env.action_space.sample()
else:
return np.argmax(q_table[state])
for i in range(num_episode):
e = 1. / (i // 100 + 1)
state = env.reset()
action = get_action(e, state)
done = False
while not done:
next_state, reward, done, _ = env.step(action)
next_action = get_action(e, next_state)
td_target = reward + gamma * q_table[next_state][next_action]
q_table[state][action] = q_table[state][action] + alpha * (td_target - q_table[state][action])
state = next_state
action = next_action
success.append(reward)
plt.bar(range(num_episode), success, color='red')
plt.show()
print('success rate:', np.mean(success))
Q-learning
Q-learning 은 off-policy TD control 알고리즘으로 벨만 최적 방정식을 이용합니다.
$Q(s,a)$ 에 대한 벨만 최적 방정식과 업데이트 식은 다음과 같습니다.
$q_*(s,a) = \mathbb{E} \left[ R_{t+1} + \gamma {\underset {a'} {max}} q_*(S_{t+1},a') | S_t=s A_t=a \right]$
$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma {\underset {a} {max}}Q(S_{t+1} ,a) - Q(S_t, A_t) \right]$
Q-learning 알고리즘은 다음과 같습니다.

구현
Q-learning 알고리즘을 구현합니다.
import matplotlib.pyplot as plt
import numpy as np
import gym
env = gym.make('FrozenLake-v0', is_slippery=False)
num_episode = 2000
gamma = 0.99
alpha = 0.01
q_table = np.zeros((env.observation_space.n, env.action_space.n))
success = []
def get_action(e, state):
if np.random.rand() < e:
return env.action_space.sample()
else:
return np.argmax(q_table[state])
for i in range(num_episode):
e = 1. / (i // 100 + 1)
state = env.reset()
done = False
while not done:
action = get_action(e, state)
next_state, reward, done, _ = env.step(action)
td_target = reward + gamma * np.max(q_table[next_state])
q_table[state][action] = q_table[state][action] + alpha * (td_target - q_table[state][action])
state = next_state
success.append(reward)
plt.plot(range(num_episode), success)
plt.show()
print('success rate:', np.mean(success))
On-policy vs Off-policy
TD 를 이용하는 제어 방법으로 off-policy TD control 알고리즘인 SARSA 와 on-policy TD control 알고리즘인 Q-learning 을 알아보았습니다.
on-policy 와 off-policy 는 어떤 차이점을 갖을까요?
on-policy 란 직접 배우는 것으로 해당 정책을 통해서 나온 경험을 이용해서 학습합니다. 또한 하나의 정책을 사용하여 계속해서 개선해 나가는 것이 특징입니다.
대표적인 on-policy 알고리즘으로는 SARSA, 1-visited MC, Actor-Critic, PPO 등이 있습니다.
off-policy 란 간접적으로 배우는 것이라고 할 수 있습니다. 간접적으로 배우기 때문에 행동 정책과 타겟 정책이 다를 수 있으며 다른 정책을 통해서 나온 경험을 이용해서 학습이 가능합니다. 따라서 과거의 경험을 사용할 수 있기 때문에 데이터 효율성이 좋다고 할 수 있습니다.
대표적인 off-policy 알고리즘으로는 Q-learning, every-visited MC, DQN, DDPG, 등이 있습니다.
SARSA vs Q-Learning
SARSA 는 벨만 기대 방정식, Q-learning 은 벨만 최적 방정식을 기반으로 했습니다.
$q_{\pi}(s,a) = \mathbb{E}_{\pi}[r_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1}) | S_t=s, A_t=a]$
$q_*(s,a) = \mathbb{E} \left[ R_{t+1} + \gamma {\underset {a'} {max}} q_*(S_{t+1},a') | S_t=s A_t=a \right]$
두 식의 가장 큰 차이라면 정책의 유무라고 할 수 있습니다. 벨만 기대 방정식에서 다음 상태의 $q_{\pi}$ 는 해당 정책을 따르는 행동 가치 함수로 해당 정책 $\pi$ 에 의존적이며 현재 상태와 다음 상태 간의 상관관계(correlation)가 크다고 할 수 있습니다. 따라서 SARSA 를 on-policy 알고리즘이라고 하는 것입니다.
반면에 벨만 최적 방정식은 다음 상태의 $q_*$ 에서 최대의 행동 가치를 이용합니다. 이는 정책 $\pi$ 과 관련없으며 해당 환경의 샘플을 이용하여 업데이트를 반복하면 최적 $q_*$ 에 수렴한다는 것입니다. 이 때문에 Q-learning 을 off-policy 알고리즘이라고 합니다.
다음과 같은 환경을 통해 on-policy 인 SARSA 와 off-policy 인 Q-learning 의 차이를 살펴볼 수 있습니다.
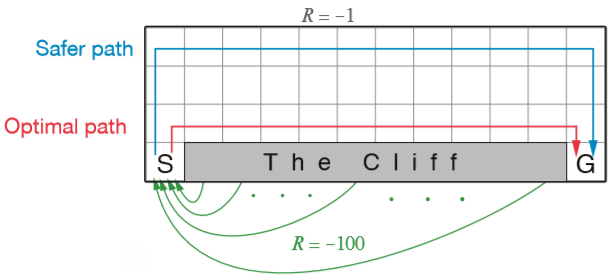
절벽으로 이동하면 -100 의 보상을 얻게되며 그 외에는 일괄적으로 -1 의 보상을 얻습니다.
구현
환경 정보를 불러오고 공통부분을 정의합니다.
# sarsa vs q-learning
from cliff_walking import CliffWalkingEnv
import numpy as np
import matplotlib.pyplot as plt
env = CliffWalkingEnv()
print('act:', env.action_space.n)
print('obs:', env.observation_space.n)
table = {
'q-learning': np.zeros((env.observation_space.n, env.action_space.n)),
'sarsa': np.zeros((env.observation_space.n, env.action_space.n))
}
result = {
'q-learning': [],
'sarsa': []
}
num_episode = 2000
decay_e = 1 / num_episode
def predict(state):
if np.random.rand() < e:
action = env.action_space.sample()
else:
action = np.argmax(q_table[state])
return action
Q-learning 알고리즘으로 $Q$ 테이블을 학습합니다.
# q-learning
q_table = table['q-learning']
gamma = 0.99
alpha = 0.1
e = 1
for i in range(num_episode):
if e > 0.1:
e -= decay_e
state = env.reset()
done = False
while not done:
action = predict(state)
next_state, reward, done, _ = env.step(action)
td_target = reward + gamma * np.max(q_table[next_state])
q_table[state, action] += alpha * (td_target - q_table[state, action])
state = next_state
# print('episode:', i, 'reward', reward)
# print(q_table)
SARSA 알고리즘으로 $Q$ 테이블을 학습합니다.
# sarsa
q_table = table['sarsa']
gamma = 0.99
alpha = 0.1
e = 1
for i in range(num_episode):
if e > 0.1:
e -= decay_e
state = env.reset()
action = predict(state)
done = False
while not done:
next_state, reward, done, _ = env.step(action)
next_action = predict(next_state)
td_target = reward + gamma * q_table[next_state, next_action]
q_table[state, action] += alpha * (td_target - q_table[state, action])
state = next_state
action = next_action
# print('episode:', i, 'reward', reward)
# print(q_table)
각 알고리즘을 통해 학습된 $Q$ 테이블을 이용해서 플레이합니다.
# play
import time
for i in range(1):
state = env.reset()
done = False
while not done:
env.render()
time.sleep(1)
action = np.argmax(table['sarsa'][state])
# action = np.argmax(table['q-learning'][state])
state, reward, done, _ = env.step(action)
print(state, reward)
Q-learning 은 최적의 경로를 통해 클리어하는 것을 볼 수 있습니다.

반면에 SARSA 는 절벽을 피해가는 경로를 이용합니다.

각 알고리즘의 테이블을 히트맵으로 확인해봅니다.
import matplotlib.pyplot as plt
import seaborn as sns
q_table = np.max(table['q-learning'], axis=1).reshape(4, 12)
sns.heatmap(np.around(q_table, 1), annot=True)
plt.title('Q-Learning', fontsize=20)
plt.show()
q_table = np.max(table['sarsa'], axis=1).reshape(4, 12)
sns.heatmap(np.around(q_table, 1), annot=True)
plt.title('SARSA', fontsize=20)
plt.show()
Q-learning 의 테이블은 최적의 경로의 상태들이 높은 가치로 기록되어 있습니다.

반대로 SARSA 의 테이블은 나쁜 보상을 주는 절벽에 근접한 상태일 수록 낮은 가치로 기록되어 있습니다.

'머신러닝 > 강화학습' 카테고리의 다른 글
| DQN(Deep Q-Networks) (1) (0) | 2020.11.20 |
|---|---|
| 함수 근사(Function Approximation) (0) | 2020.11.18 |
| 소프트맥스 회귀(Softmax Regression) (2) (0) | 2020.11.12 |
| Model-Free Prediction (0) | 2020.11.09 |
| OpenAI Gym (0) | 2020.11.09 |