가중치 초기화(Weight Initialization)
과대적합(Overfitting)을 억제하는 기법으로 은닉층을 이루는 가중치의 초기값을 0이 아닌 최대한 작은 값에서 시작하는 것입니다. 이는 활성화 함수에 따라 다른 방법을 사용합니다.
활성화 함수로 시그모이드(Sigmoid)를 사용하는 경우에 권장하는 방법으로 Xavier 초기화 방법이 있습니다. Xavier는 표준편차가 $ \sqrt{ 1 \over n } $ 인 정규분포를 이용합니다. ($n$ 은 앞 계층의 노드 수)
활성화 함수로 렐루(ReLU)를 사용하는 경우에는 He 초기화 방법이 있습니다. He는 표준편차가 $ \sqrt{ 2 \over n } $ 인 정규분포를 이용합니다. 2배의 계수로 인해 Xavier 보다 더 넓게 분포할 것입니다.
구현
가중치 초기화 방법에 따른 활성화 분포를 비교를 하기 위한 시각화를 구현합니다.
import numpy as np
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 3))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def relu(x):
return np.maximum(x, 0)
def weight_initialize(node_num, std=1):
return np.random.randn(node_num, node_num) * std
def forward(title, init, activation_function, hidden_layer_size=5):
activations = []
x = np.random.randn(1000, 100)
for i in range(hidden_layer_size):
w = init
z = np.dot(x, w)
a = activation_function(z)
activations.append(a)
x = a
fig, axs = plt.subplots(1, len(activations), constrained_layout=True, sharey=True)
plt.ylim(0, 10000)
for i, layer in enumerate(activations):
axs[i].hist(layer.flatten(), 20, range=(0, 1))
axs[i].set_xlabel('{}-layer'.format(str(i+1)))
fig.suptitle(title)
시그모이드 함수를 사용하는 경우에 표준편차 1, 0.01, $ \sqrt{ 1 \over n } $ (Xavier) 초기화에 따른 분포를 비교합니다.
# sigmoid, activations
node_num = 100
init = weight_initialize(node_num)
forward('std=1', init, sigmoid)
init = weight_initialize(node_num, 0.01)
forward('std=0.01', init, sigmoid)
xavier = (1 / np.sqrt(node_num))
init = weight_initialize(node_num, xavier)
forward('Xavier', init, sigmoid)
표준편차를 0.01로 하였을 경우, 분포가 0.5에 집중된 것을 볼 수 있습니다. 이는 많은 가중치를 갖는 의미가 없는 것입니다.
렐루 함수를 사용하는 경우에 표준편차 0.01, $ \sqrt{ 1 \over n } $ (Xavier), $ \sqrt{ 2 \over n } $ (He) 초기화에 따른 분포를 비교합니다.
# relu, activations
node_num = 100
init = weight_initialize(node_num, 0.01)
forward('std=0.01', init, relu)
xavier = (1 / np.sqrt(node_num))
init = weight_initialize(node_num, xavier)
forward('Xavier', init, relu)
he = (np.sqrt(2 / node_num))
init = weight_initialize(node_num, he)
forward('He', init, relu)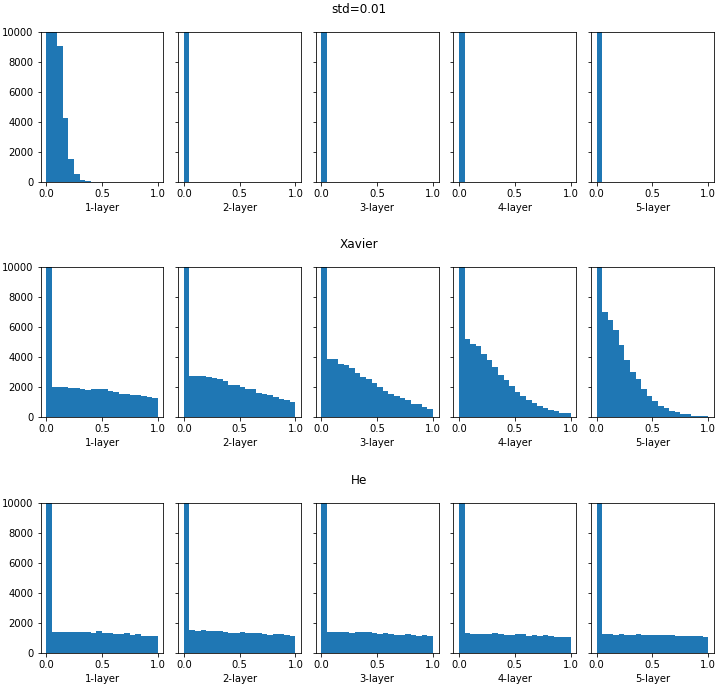
각 층의 분포를 살펴보면, 표준편차가 0.01인 경우에는 거의 학습이 이루어지지 않을 것입니다. 활성화 값은 0에 가까운 작은 값이며, 학습시에 역으로 전파되는 가중치의 기울기 역시 매우 작다는 것입니다. Xavier인 경우에도 층이 깊어지면서 활성화 값이 점점 0으로 편향되는 것을 볼 수 있습니다. 이와 같은 현상은 학습시에 기울기 소실(Gradient Vanishing) 문제를 일으키는 것입니다.
은닉층의 크기를 10으로 지정해보면 더욱 큰 차이를 나타냅니다.
node_num = 100
xavier = (1 / np.sqrt(node_num))
init = weight_initialize(node_num, xavier)
forward('Xavier', init, relu, 10)
he = (np.sqrt(2 / node_num))
init = weight_initialize(node_num, he)
forward('He', init, relu, 10)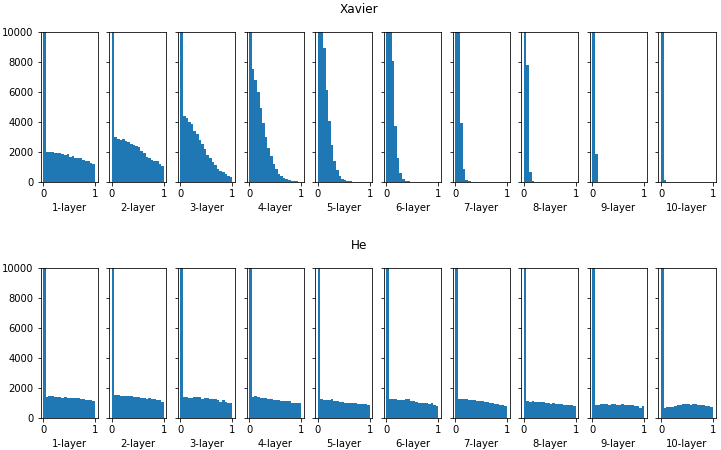
이에 반해 He는 층이 깊어져도 고르게 분포되는 것을 볼 수 있습니다.
'머신러닝 > 딥러닝' 카테고리의 다른 글
| 가중치 규제(Weight Regularization) (0) | 2021.02.09 |
|---|---|
| 배치 정규화(Batch Normalization) (0) | 2021.02.09 |
| LSTM(Long Short-Term Memory) (0) | 2021.02.03 |
| 순환 신경망(Recurrent Neural Network) (3) (0) | 2021.01.12 |
| 순환 신경망(Recurrent Neural Network) (2) (0) | 2021.01.04 |